Description

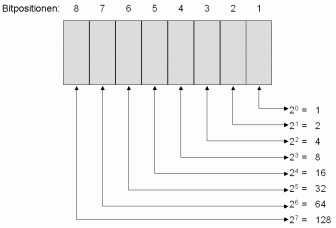
Supongamos que tenemos un número binario de 4 bits [a3 a2 a1 a0] su valor decimal correspondería al valor que resulta de 8a3 + 4a2 + 2a1 + 1a0, por lo que se puede decir que el vector de factores multiplicativos de un número binario de 4 bits comúnmente aplicado es [8, 4, 2, 1]. Sin embargo podemos utilizar otro vector de factores multiplicativos para el caso particular de un número binario de 4 bits como por ejemplo [4, 8, 1, 2] o también [1, 3, 5, 10]. Ve la siguiente tabla para ver cómo afecta al valor decimal representado cambiando los factores.

Algo que tienen en común es que cualquiera de los 3 vectores multiplicativos usados en la tabla previa, asocian a un número decimal de una única forma o no lo pueden asociar (por ejemplo, el número 2 decimal no puede ser representado como un número binario de 4 bits usando el vector [1,3,5,10]). Por otra parte si utilizamos el vector [1,2,3,4], el número decimal 6 puede ser representado con los números binarios de 4 bits: 1110 y 0101.

Tu problema consiste dado la base b (1 < b < 11), el número de dígitos n (n ≤ 1000), y un vector de factores multiplicativos [e1 e2 … en]. Decidir si existen números que tienen más de una representación.

Puedes estar seguro que (b-1) (e1 + e2 + … + en) ≤ 10,000,000.

Input

La entrada consiste primero de una línea que un entero nc (0 < nc ≤ 100) que indica el número de casos a procesar. Cada línea siguiente corresponde a un único caso de entrada con los valores de b, n y e1, e2, …, en descritos antes.

Output

Por cada caso imprime una línea con el mensaje ‘YES’ si existen números que tienen más de una representación, ‘NO’ en otro caso. Ve el ejemplo de entrada y salida para mas detalle.

4
2 4 8 4 2 1
2 4 4 8 1 2
2 4 1 3 5 10
2 4 1 2 3 4

NO
NO
NO
YES

Problemsetter: Gabriel Filiberto López Pérez