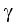 are constant).
are constant).
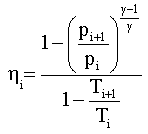
![]()
| Problem A: Multi-stage Compressor |
| Time Limit: 1 second |
As part of an engeener team in ACM (Association for Compressors and Machinery) you're working in an air-condition system for a plane. As ambient air at 10km over surface is too cold, you have to mix it with some hot air from the engine.
To design the system, you need to know the pressure of the hot air at the bleeding point. You're supposed to bleed the air from one of the stages of the compressor in the engine. Unfortunately, you don't know pressures at intermediate stages, you can only measure pressure at the begining of the compressor. So, in this problem you'll have to calculate pressure at stage i.
About the compressor, you know:
Its global pressure ratio, that is, the pressure at the end of the compressor (pn+1)divided by the ambient pressure(p1). Since you know ambient pressure, you can easily calculate the pressure at the end of the compressor. The air is a perfect gas (that is, parameters cp and are constant).
After every stage of the compressor, there is a system that turns air's temperature, Ti, into ambient air temperature, T1. We suppose there's no pressure loss in this process. The compressor has some constant (unknown) parametes: i (efficiency) and
(the mass of air entering in the compressor each second).
i is defined as:
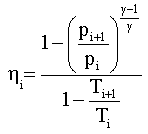
Compressor's global power needed is minimum. Power for each stage is defined as:
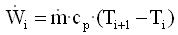
With all these, stage i's representation is as follows:
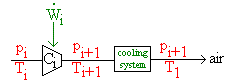
The first line of input gives the number of cases, N. N test cases follow. Each one is a line containing n (the number of stages), p1 (p1 > 0) (ambient pressure), pn+1 (pn+1 ≥ p1) (final pressure) and i (with 1 ≤ i ≤ n+1) (the stage you bleed air from).
For each test case, output one line containing pi, the pressure at stage i with two decimals of precision.
Sample input |
Sample output |
|---|---|
3 2 1 2 1 2 1 2 2 2 1 2 3 |
1.00 1.41 2.00 |